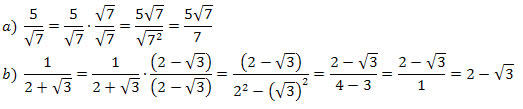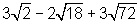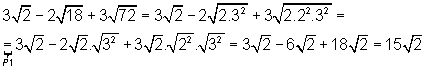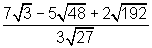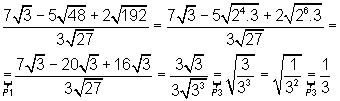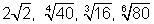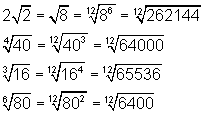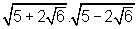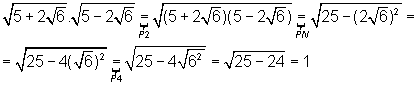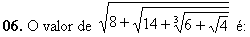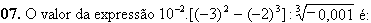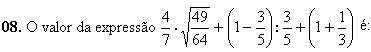Prismas - definição 

Prisma é um poliedro convexo tal que duas faces são polígonos congruentes situados em planos paralelos e as demais faces são paralelogramos.





Prismas - Nomenclatura e Classificação 

Os prismas recebem nomes de acordo com os polígonos das bases.

Assim,

• um prisma é triangular quando suas bases são triângulos;

• um prisma é quadrangular quando suas bases são quadriláteros;

• um prisma é pentagonal quando suas bases são pentagonais;

• um prisma é hexagonal quando suas bases são hexagonais.


Quando as arestas laterais de um prisma forem perpendiculares aos planos das bases, o prisma é chamado de reto; caso contrário, de oblíquo.

Os prismas retos cujas bases são polígonos regulares são chamados de prismas regulares.

Exemplos

Prismas regulares

Cubo
Cubo- Definição e Elementos

Cubo é um prisma em que todas as faces são quadradas. O cubo é um prisma quadrangular regular cuja altura é igual à medida da aresta da base.
O cubo da figura tem arestas de medida l então, 
• as diagonais de suas faces medem l 
, pois são diagonais de quadrados de lados com medidas iguais a l.
 

• as diagonais do cubo medem l Raiz cúbica , pois:




Assim: 
Área TotalA área de um quadrado de lado l é l 2, então a área A da superfície de um cubo de aresta l é:


Paralelepípedos - Definição

Chamamos de paralelepípedo o prisma cujas bases são paralelogramos; dessa forma, todas as faces de um paralelepípedo são paralelogramos.

Exemplos



Paralelepípedo Reto Retângulo


Diagonais de um paralelepípedo retângulo
No paralelepípedo da figura com dimensões a, b e c, sejam d1 e d, as diagonais da face ABCD e do paralelepípedo, respectivamente.






No triângulo ABC, temos:

AC2 = AB2 + BC2
ou então,



No triângulo ACG, temos:
AG2 = AC2 + CG2

ou então,
Como
, temos:
d2 = a2 + c2 + b2 ou



Área total (AT) de um
paralelepípedo retângulo

Sendo a, b e c as dimensões de um paralelepípedo retângulo, as áreas de cada par de faces opostas são: ab, ac e bc. 
Assim,
Ou







Volume (V) de um paralelepípedo retângulo

Sendo a, b e c as dimensões do paralelepípedo retângulo, temos:

Área e Volume de Prismas Regulares

Sabemos que um prisma é chamado de regular quando é reto e tem base regular.

Vamos calcular a área e o volume dos principais prismas regulares:

Prisma Triangular Regular

Consideremos um prisma triangular regular com aresta da base a e altura h.

Área da base (B)
Área lateral (AL)AL = 3 • A face lateral
AL = 3 • (ah)= 3 ah
Área total (AT)
AT = AL + 2B








Volume (V)

V = S . h


V = B • h

Prisma Hexagonal Regular

Consideremos um prisma hexagonal regular com aresta da base a e altura h.

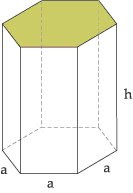Área da Base (B)
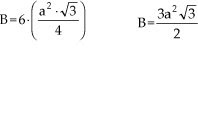Área lateral (AL)


AL = 6 • Aface lateral

AL = 6 (ah) = 6 ah

Área total (AT)

AT = AL + 2B




Volume (V)

V = B • h

Questões resolvidas de vestibulares sobre Prismas

1) Um prisma de base quadrangular possui volume igual a 192 cm³. Determine sua altura sabendo que ela corresponde ao triplo da medida da aresta da base. 

Solução: 

Aresta da base: x cm
Altura: 3x cm
Volume: 192
V = x * x * 3x
3x³ = 192
x³ = 192/3
x³ = 64
x = 4
Altura: 3 * 4 = 12 cm
A altura do prisma de base é correspondente a 121 cm.

2) Um prisma reto tem por base um triângulo isósceles de 8cm de base por 3cm de altura. Sabendo que a altura do prisma é igual a 1/3 do perímetro da base, calcule sua superfície total. 

Solução:

No triângulo isósceles a altura também é mediana. 

i) Pela relação de Pitágoras temos: 

logo a = 5cm

ii) O perímetro da base vale: 5cm + 5cm + 8cm = 18cm
iii) A altura do prisma vale 
1/3 x 18 = 6cm
iv) área total
Ab = 8 x 3 /2 = 12cm²
Al = (8x6)+2 x (5x6) = 108cm²
At= 2x 12 + 108= 132cm²

3) Em um prisma regular triangular, cada aresta lateral mede 10 cm e cada aresta da base mede 6 cm. Calcular desse Prisma:

a) a área de uma face lateral.
b) a área lateral.
c) a área total.










Solução:

a) Af = (6.10) cm²
    Af = 60 cm²

b) A área lateral AL é a soma das áreas das três fases laterais, isto é:

AL = 3 . Af
AL = 3 . 60 cm²
AL = 180 cm²

c) A área total At é a soma da área lateral AL com duas vezes a área B de uma base, isto é:

At = AL + 2B
At = (180 + 18 √3) cm²

4) Em uma piscina regular hexagonal cada aresta lateral mede 8 dm e cada aresta da base mede 4 dm. Calcule, desses prisma:

a) a área de cada face lateral;
b) a área de uma base;
c) a área lateral;
d) a área total;





Solução:


a) Af = b . h
    Af = 4 .8
    Af = 32 dm²

b) Ab = (6.10 √3) / 4
    Ab = 24 √3 dm²

c) AL = 6.4.8
   AL = 192 dm²

d) At = 2.24 √3 +192
    At = 48 √3 + 192 dm²

5) (PUC-SP) Um tanque de uso industrial tem a forma de um prisma cuja base é um trapézio isósceles. Na figura a seguir, são dadas as dimensões do prisma em metros:

O volume desse tanque em metros cúbicos é:

a)      50 b)      60

c)      80 d)      100

e)      120

Solução:

a = cateto do triângulo retângulo formado com a altura do trapézio isósceles.

a=(8-2)/2⇒a=3 
h = altura do triângulo.
h²+3²=5²⇒h²=16⇒h=4 
A_b = área da base do prisma (tanque)

A_b=(8+2)4/2⇒A_b=20 
V = volume do prisma

V=20*5⇒V=100 

Resposta = d)

6)  Um prisma pentagonal regular tem 20cm de altura. A aresta da base mede 4cm. Determine sua área lateral. 

Solução:

 A área lateral é a soma das cinco áreas dos retângulos que são as faces laterais. Como a base é regular, todas as arestas possuem a mesma medida. Logo, temos:
i) Área de uma face: 4 x 20 = 80cm2
ii) Área lateral: 5 x (80cm2) = 400cm2.


7) Um prisma quadrangular regular tem sua aresta da base medindo 6m. Sabendo que a área lateral do prisma mede 216m², calcule sua altura. 

Solução: 

Se o prisma é regular então suas bases são quadradas. A área lateral é a soma das áreas das quatro faces. Temos:
216 = 4x6xh
h =216/24 h = 9

8) Um prisma reto tem por base um triângulo isósceles de 8cm de base por 3cm de altura. Sabendo que a altura do prisma é igual a 1/3 do perímetro da base, calcule sua superfície total. 

Solução:

No triângulo isósceles a altura também é mediana. 

i) Pela relação de Pitágoras temos: 

logo a = 5cm

ii) O perímetro da base vale: 5cm + 5cm + 8cm = 18cm

iii) A altura do prisma vale 

1/3 x 18 = 6cm

iv) área total

Ab = 8 x 3 /2 = 12cm²

Al = (8x6)+2 x (5x6) = 108cm²

At= 2x 12 + 108= 132cm²

9) Calcule a área total de um prisma reto, de 10 cm de altura, cuja base é um hexágono regular de 6cm de lado. 

Solução:

A área total de um hexágono regular vale o sêxtuplo da área do triângulo equilátero. 

Temos: . 

Ab =6x (6²x ṛaiz quadrada de3)/4 = 93,5

Al = 6x6x10 = 360

At = 2 x93,5 +360 = 547cm²

Radiciação - Propriedades e operações

Radiciação - Propriedades e operações 

Radiciação

A radiciação é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões aritméticas e algébricas. Vamos definir essa operação e analisar suas propriedades.
Dados um número real não negativo x e um número natural n ≥ 1, chama-se raiz enésima de x o número real não negativo y tal que yⁿ = x. O símbolo utilizado para representar a raiz enésima de x é  e é chamado de radical. Nesse símbolo, x é o radicando e n é o índice.

Pela definição de radiciação, temos que:

Exemplo 1:

Propriedades da radiciação

Exemplo 2. Simplifique a expressão

Exemplo 3. Verifique as propriedades da radiciação.

Exemplo 4. Obtenha a forma mais reduzida possível da expressão:

Solução: Podemos reescrever cada uma das raízes utilizando as propriedades da radiciação.

Racionalização de denominadores

Em alguns cálculos, você pode se deparar com raízes no denominador da fração. Para que você possa prosseguir com os cálculos, é conveniente que você elimine essas raízes do denominador - processo chamado de racionalização de denominadores. Isto é, transforma-se um denominador irracional em racional.

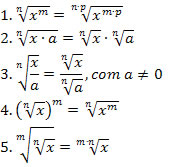
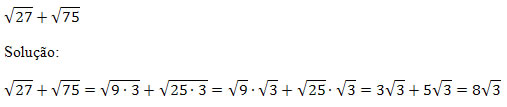
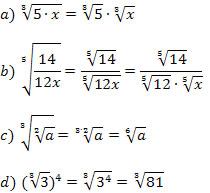
 o denominador  é um número irracional e deve ser eliminado.

Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.

Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por  ficará:

. Note que  é igual a 1, logo a multiplicação de um número por 1 não o altera.

Prosseguindo:

Como se pode notar o denominador agora é um número racional (3).

Raízes não-quadradas

Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz quadrada é, na verdade, uma raiz de índice 2!), é necessário utilizar um artifício.

Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original menos um. Por exemplo:

Soma de raízes no denominador

Veja:

Deve-se multiplicar por .

Isso porque a multiplicação de  por  é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a² - b²) - isto é, os radicais somem!

Exemplo 1. Racionalize as seguintes frações:

Racionalizar a fração é fazer com que no denominador não exista uma raiz enésima de um número. 

Exemplo 2. Racionalize as frações:

Operações com radicais

Radicais como potências de expoente fraccionário         

             

São da forma ⁿ√a^m =a ^m/n , com a>0, n ∈ ℕe m/n ∈ℚ  

                

Exemplos:

                        ⁵√2^-3 = 2^-3/5

                        3⁵ =3 ^15/3 = ³ √(3 ¹⁵)       

                       2 ^–1/4 = (1/2)^1/4 = ⁴√(1/2) ou 2^-1/4 =⁴√2^-1

Multiplicação de  radicais

         

Aqui, os radicais têm que ter o mesmo índice, sendo da forma  

ⁿ√a´ⁿ√b = ⁿ√(ab)

  com a, b ∈ ℝ⁺ e n∈ℕ.

            Exemplos:

                     √2´√3´√5 = √(2´3)´√5 = √6´√5 = √(6´5) = √30

                     √2´⁴√3 = ^2´2√2² ´⁴√3 = ⁴√4´ ⁴√3 = ⁴√12

          

Divisão de radicais    

           

Tal como na multiplicação, também os radicais aqui  têm de ter o mesmo índice. Assim, são da forma

  ⁿ√a ¸ⁿ√b = ⁿ√ (a/b)

  com a, b ∈ℝ⁺ e n∈ℕ.

           

 Exemplo:

                    ³√6 ¸ ³√3´³√2 = ³√ (6/3)´³√2 = ³√2´³√2 = ³√4

         

Adição de expressões com radicais     

            

Só é possível simplificar a soma de expressões com radicais se estes tiverem o mesmo índice e o mesmo radicando. As operações de simplificação de radicais são: divisão do índice do radical e o expoente do radicando pelo seu máximo divisor comum ou passagem para fora do radical todos os factores possíveis.

 Exemplos:

                    √2-√5+3√2+7√5 = √2+3√2-√5+7√5 = (1+3) √2+(-1+7)√5 = 4√2+6√5

                    ³√5+2⁹√5³ = ³√5 + 2³√5  = (1+2) ³√5  = 3 ³√5 

                           pois 2⁹√5³ = 2^9:3√5^3:3 =2³√5 

                     5√18+2√2 = 15√2 + 2√2 = (15+2)√2 = 17√2

                           pois 5√18 = 5√(3² ´2) = 5√3²´√2 = 5´3√2 = 15√2

                              

Passagem de um  fator para fora de um radical  

             

Decompõe-se o radicando num produto de factores primos e aplica-se a propriedade da multiplicação de radicais.Para passar um factor para dentro do radical eleva-se este ao índice do radical.

  Exemplos:

                    √108

108|   2

  54 |  2

  27|  3

    9| 3

     3| 3

  1|

então  √108 = √ (2²´3²´3) = √2²´√3³´√3 = 2´3´√3 = 6√3

                    2√5 = √(2²´5) = √20

                    3³√5² = ³√(3³´5²) = ³√(27´25) = ³√675

         

Potência de um radical

             

A potência de um radical tem a forma  (ⁿ√a)^p = ⁿ√(a^p) com a>o e n, p ∈ℕ.

                  

Exemplos:

                           (⁶√2)⁵ = ⁶√2⁵

         

 Radical de um radical

            

  É da forma ⁿ√(^p√a )= ^np√a com a>o e n, p ∈ℕ

                  

Exemplos:

                          ⁵√(√3) = ^2´5√3 = ¹⁰√3

Fonte: www.mundovestibular.com.br

            www.educaçao.uol.com.br
            http://www.educ.fc.ul.pt/

Questões sobre radiciação e racionalização de denominadores

01. (UFCE) Simplificar a expressão:

Solução:

Exercício simples que se baseia na decomposição em fatores primos de cada radicando e da utilização da propriedade P1, como você pode observar no detalhamento a seguir. Tenha em conta que na soma ou subtração de radicais, cada parcela deve ser considerada isoladamente para se obter o resultado de uma expressão. Ou seja, não se aplica que a soma de duas raízes de mesmo índice é igual a raiz da soma, como é o caso do produto, por exemplo.

02. Calcular o quociente:

Solução:

Outro exercício de solução simples onde demonstro o uso das propriedades P1 e P3, e novamente, faço uso da decomposição em fatores primos dos radicandos:

03. Escrever em ordem de grandeza crescente os radicais:

Solução:

Para fazer a comparação entre os radicais devemos, inicialmente, reduzí-los ao mesmo índice. Isto é feito calculando o mínimo múltiplo comum (mmc) dos índices e, após, aplicando a propriedade P6. O mmc(2, 4, 3, 6) = 12 e reescrevendo os radicais (P6) vem:

Agora, basta considerar a ordem dos radicandos para estabelecer a ordem crescente dos radicais:

04. Efetuar

Solução:

Esboçada a seguir, onde utilizamos o fato de que o produto da soma pela diferença de dois números é igual ao quadrado do primeiro menos o quadrado do segundo (produto notável – PN) e as propriedades da Radiciação indicadas:

05. Simplifique a expressão:

 

a) -0,1

b) -1,7

c) -17

d) 0,1

e) 1,7

a) 0,4

b) 2,5

c) a

d) 1,5

e) 1

09. Escreva simplificadamente:

a) 

b) 

c) 

10) Calcule .

11)  Calcule .

12) Simplifique o radical 

13) (F. C. Chagas-SP) O número  √2352 corresponde a: 

a) 4  √7 . 
b) 4  √21 . 
c) 28  √3 . 
d) 28  √21 . 
e) 56  √3 .

14) (UFSC) O valor de  x, que satisfaz a equação  22x + 1 – 3 . 2x + 2 = 32, é:

15) (Fuvest)    é igual a:

16) (UFSC)  Dê o somatório da(s) proposição(ões) VERDADEIRA(S).

Gabarito:

06) A  07) B  08) B  09)  a) 

b)           c)    

10) 25     11) 49    12)    14) x = 3   15) E
16) 2 + 8 + 16 + 64 = 90